Exercice 61 page 285

• Les cinq chansons constituent une répétition d'expériences aléatoires identiques et indépendantes. Pour chacune la probabilité de playback est de $0,89$ et celle de direct est de $0,11$.

• La probabilité que l'artiste utilise le direct cinq fois de suite est donc de $0,11^5$.

Exercice 62 page 285

• Un groupe de sept personnes âgées de plus de 75 ans pour lesquels on détermine s'ils sont malades d'Alzheimer, constitue la répétition d'expériences aléatoires identiques et indépendantes. Pour chacune la probabilité d'être malade d'Alzheimer est de $0,18$ et celle de n'être pas malade est de $0,82$.

• L'événement "Au moins une personne du groupe est malade" est le contraire de l'événement "Toutes les personnes ne sont pas malades" dont la probabilité est $0,18^5$.

• La probabilité qu' "Au moins une personne du groupe est malade" est donc de $1 - 0,18^5$.

Exercice 64 page 285

• Les lancers francs successivement tentés par Clara constituent la répétition d'expériences aléatoires identiques et indépendantes. Pour chaque lancer la probabilité de réussite est de $0,15$ et sa probabilité d'échec est de $0,85$.

• L'événement "Elle ne réussit aucun lancer franc sur n lancers" a donc pour probabilité $0,85^n$.

• Avec la calculatrice, on peut faire un tableau de valeurs de la fonction Y = 0.85 ^ X en commençant à $1$ avec un pas de $1$ et on trouve que le plus petit entier $n$ tel que $0,85 ^n < 0,01$ est $n =29$.

• On peut aussi programmer un algorithme de seuil, sur TI par exemple (les symboles ne sont pas corrects) :

  0.85 -> P
  1 -> N
  While P >= 0.01
  0.85 * P -> P
  N + 1 -> N
  End
  Disp N

Exercice 70 page 285

• Un groupe de dix Français pour lesquels on détermine leur groupe sanguin, constitue la répétition d'expériences aléatoires identiques et indépendantes. Pour chaque individu la probabilité qu'il soit du groupe O est de $0,43$ et la probabilité qu'il ne soit pas du groupe O est de $0,57$

• L'événement "Aucun des dix n'est du groupe O" a pour probabilité $0,57^{10}$.

• L'événement contraire "Au moins un des membres est du groupe O" a donc pour probabilité $1 - 0,57^{10}$.

Exercice 89 page 293

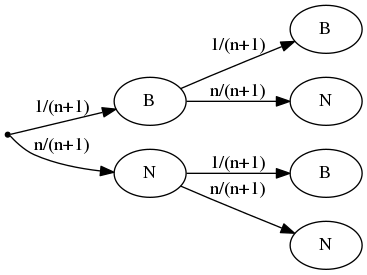
Arbre Pondéré de l'exo 89p.293

1. La variable aléatoire $G$ donnant le gain d'Oriane peut prendre trois valeurs : $1$, $10$ et $-3,5$.

   • $\mathbb{P}(G = 1) = \mathbb{P} ( [N, N] ) = \frac{n}{n+1} \times \frac{n}{n+1} = \frac{n^2}{(n+1)^{2}}$

   • $\mathbb{P}(G = 10) = \mathbb{P} ( [B, B] ) = \frac{1}{n+1} \times \frac{1}{n+1} = \frac{1}{(n+1)^{2}}$

   • $\mathbb{P}(G = -3,5) = \mathbb{P} ( [N, B] \cup [B, N]) = 2 \times \frac{1}{n+1} \times \frac{n}{n+1} = \frac{2n}{(n+1)^{2}}$

2. On en déduit l'espérance mathématique de $G$ : $$\mathbb{E} (G) = 1 \times \frac{n^2}{(n+1)^{2}} + 10 \times \frac{1}{(n+1)^{2}} - 3,5 \times \frac{2n}{(n+1)^{2}} = \frac{n^2 - 7n + 10}{(n+1)^{2}}$$

3. Le jeu est équitable si et seulement si $\mathbb{E} (G) = 0$. Résolvons l'équation : $$\mathbb{E} (G) = 0 \Longleftrightarrow n^2 - 7n + 10 = 0$$ On calcule le discriminant : $\Delta = (-7)^{2} - 4 \times 10 = 9$.

   $\Delta >0$ donc l'équation a deux racines distinctes et on trouve $n = 5$ ou $n = 2$.

   Le jeu est donc équitable si on a $2$ ou $5$ boules blanches dans l'urne.

4. Le jeu est favorable à Adrien si et seulement si $\mathbb{E} (G) < 0 \Longleftrightarrow n^2 - 7n + 10 < 0$.

   D'après la règle du signe d'un trinôme, c'est le cas uniquement pour les entiers positifs entre $2$ et $5$ compris donc pour $2$,$3$,$4$ et $5$.