Rentrée
Séance du 05/09/2016
Chapitre 1 Rappels sur l'ordre, Généralités sur les suites et récurrence
- Présentation du programme, des objectifs, consignes de matériel (1 cahier grand format pour le cours et un cahier ou classeur pour les exercices, calculatrice)
- Cours :
- Rappels de calculs : étude de la série harmonique, somme télescopique (exemple 1), programmation de la calculatrice, algorithme de seuil, résolution d'inéquation du second degré.
- DM n°1 .
- Jeudi 15/09 : DS n°1 sur les suites, durée 1 h.
Séance du 06/09/2016
Chapitre 1 Rappels sur l'ordre, Généralités sur les suites et récurrence
- Récolte du DM n°1
- Cours :
- Rappels de calculs : expressions conjuguées (exemple 2).
- Rappels sur l'ordre : ordre et opérations (exemple 3), méthode de la différence (exemple 4 1) , ordre et fonctions de référence (exemple 5 2)
- Généralités sur les suites :
- exemple 7 : (calcul des termes d'une suite récurrente, voir tutoriels sur mon site).
- Suites monotones : définition + exemple 8 (début, étude du sesn de variation de \( (u_{n}) \) avec \( (u_{n+1} - u_{n}) \) ou \( \frac{u_{n+1}}{u_{n}} \).
- Finir l'exemple 8 du cours et l'exo 1 de la fiche 1 d'exercices
- Jeudi 15/09 : DS n°1 sur les suites, durée 1 h.
Séance du 08/09/2016
Cours en classe entière
Chapitre 1 Rappels sur l'ordre, Généralités sur les suites et récurrence
- Cours :
- Généralités sur les suites :
- Suites monotones : correction de l'exemple 8 (début, étude du sens de variation de \( (u_{n}) \) avec \( u_{n+1} - u_{n} \) ou \( \frac{u_{n+1}}{u_{n}} \).
- Suites bornées : exemple 9 de 1. à 4.
- Suites arithmétiques : définitions, propriétés et exemple 10.
- Généralités sur les suites :
Cours en demi-groupe
- Suites arithmético-géométriques : définitions, propriétés et exemple 11 du cours.
- Exercice type Bac avec prise d'initiative : exemple 12 du cours.
- Suites bornées : exo 19 p. 20.
- Finir l'exemple 12.
- Lire les pages 12 et 13 du manuel sur le raisonnement par récurrence.
- Jeudi 15/09 : DS n°1 sur les suites, durée 1 h (pas de récurrence)
Séance du 12/09/2016
Chapitre 1 Rappels sur l'ordre, Généralités sur les suites et récurrence
- Cours : correction de l'exemple 12 (exercice avec prise d'initiative).
- Correction de l'exo 19 p. 20 (suites bornées).
- Correction d'exercices : suites arithmético-géométriques, exo 2 de la la fiche 1 d'exercices avec un premier exemple simple de raisonnement par récurrence.
- Faire l'exo 4 de la la fiche 1 d'exercices et faire l'exo 4 de la même fiche (révision pour le DS de jeudi)
- Jeudi 15/09 : DS n°1 sur les suites, durée 1 h (pas de récurrence)
Séance du 13/09/2016
Chapitre 1 Rappels sur l'ordre, Généralités sur les suites et récurrence
- Correction d'exercices : suites arithmético-géométriques, exo 2 de la la fiche 1 d'exercices avec un premier exemple simple de raisonnement par récurrence.
- Cours : raisonnement par récurrence
- Exemple 13 : introduction à partir de l'exemple de la formule \(\sum_{k=1}^{n}k^{2}=\frac{n(n+1)(2n+1)}{6}\)
- Exemple 14 : importance de l'initialisation.
- Suites arithmético-géométrique : correction de l'exo 4 de la fiche 1 d'exercices
- Faire les exos 14 p.19 et 51 p. 22.
- Jeudi 15/09 : DS n°1 sur les suites, durée 1 h (pas de récurrence)
Séance du 14/09/2016
Chapitre 1 Rappels sur l'ordre, Généralités sur les suites et récurrence
- Exercices du manuel sur le raisonnement par récurrence :
- Preuve d'égalité par récurrence : exo 14 p. 19 (suite arithmético-géométrique).
- Preuve d'inégalité par récurrence et sens de variation : exo 51 p. 22.
- Recherche d'exercices : exo 5 de la la fiche 1 d'exercices : tableur, suite arithmético-géométrique, second exemple de raisonnement par récurrence.
- Jeudi 15/09 : DS n°1 sur les suites, durée 1 h (pas de récurrence)
- Pour le lundi 19/09, faire sur feuille un exercice au choix du DM n°2
Séance du 15/09/2016
DS n°1 sur les suites, durée 1 h (pas de récurrence)
Chapitre 2 Limites de suites
- Fin de l'exercice 5 de la fiche 1 d'exercices
AP
- Exercice de soutien : AP1 page 28, analuse critique d'une copie.
- Exercice de niveau intermédiaire : exo 3 de la fiche 1 d'exercices
- Exercice d'approfondissement : AP3 page 29, suite de Fibonacci, récurrence forte.
- Pour le lundi 19/09, faire sur feuille les deux premiers exercices du DM n°2
Séance du 19/09/2016
Chapitre 2 Limites de suites
- Retour du DS n°1.
- Exercice : Vérifier ses acquis : 1 et 4 p. 30.
- Cours :
- Suites convergentes et divergentes : définitions et exemple 1 (algorithmes de seuil)
- Limites des suites de référence \(n^{p}, \frac{1}{n}, \sqrt{n}\)
- Refaire l'exo 1 du DS n°1.
- Faire sur feuille les deux premiers exercices du DM n°2
Séance du 20/09/2016
Chapitre 2 Limites de suites
- Récolte du DM n°2.
- Correction par les élèves de l'exo 1 du DS n°1 (suite arithmético-géométrique) et distribution d'un corrigé écrit.
- Cours :
- Exemple 1 : un exemple de suite \((-1)^{n}\) n'admettant pas de limite.
- Exemple 2 : suite arithmético-géométrique, algorithme de seuil, raisonnement par récurrence.
- Régles opératoires sur les limites : tableau synoptique.
- Lecture et commentaire du Savoir Faire 4 p. 37.
- correction de quelques exercices du manuel sur les limites de suites.
- Pour lundi prochain, DM n°3.
- Pour jeudi, faire les exercices sur l'application des règles opératoires : exo 17 p. 49 de a) à d) , exo 18 de a) à d), exo 19 a) b) et c).
- Pour jeudi lire le Savoir Faire 5 p. 37 et faire l'exo 22 p. 50 a) et b) et l'exo 23 p. 50 a) b) c).
Séance du 22/09/2016
Chapitre 2 Limites de suites
- Applications des règles opératoires sur les limites :
- Aapplication directe des règles opératoires : exo 17 p. 49 de a) à d) , exo 18 de a) à d), exo 19 a) b) et c).
- Formes indéterminées : Savoir Faire 5 p. 37 et faire l'exo 22 p. 50 a) et b) et l'exo 23 p. 50 a) b) c).
- Exemple 3 : calculs de limites avec formes indéterminées, lire le Savoir Faire 5 p. 37.
- Passage à la limite dans une inégalité, exemple 4 (Vrai/Faux) avec quelques raisonnements par l'absurde.
- Si \(u_{n}\) croissante converge vers \(\ell\) alors tous les termes de \(u_{n}\) sont inférieurs ou égaux à \(\ell\) : propriété + exemple 5.
AP : TP INFO n° 1
- Pour mardi prochain, DM n°3.
Séance du 26/09/2016
Chapitre 2 Limites de suites
- Cours :
- Limite par comparaison : propriété (preuve ROC) + exemple 6 (pas terminé).
- correction de quelques exercices du manuel sur les limites de suites.
- Pour mardi , DM n°3.
Séance du 27/09/2016
Chapitre 2 Limites de suites
- Récolte du DM n°3.
- Cours :
- Limite par comparaison : fin de l'exemple 6.
- Limite par encadrement : propriété + exemple 7.
- Limite par comparaison ou encadrement : puis exo 68 page 55.
- Cours : limite de suites géométriques : propriété 4 (inégalité de Bernoulli avec preuve ROC) .
- correction de quelques exercices du manuel sur les limites de suites.
- Exercice : (Métropole Septembre 2016) : soit une suite \((u_{n})\) de premier terme \(u_{0}\) différent de 0 et 1 et telle que pour tout entier \( n \geqslant 0 \) on a \(u_{n+1}=1-\frac{1}{u_{n}}\)
- En utilisant le mode
Suitede la calculatrice, calculer les termes de \(u_{0}\) à \(u_{12}\) de cette suite pour plusieurs valeurs de \(u_{0}\). Quelle conjecture peut-on faire sur les termes \(u_{n}\) ? - Démontrer cette conjecture.
- En utilisant le mode
Séance du 28/09/2016
Chapitre 2 Limites de suites
- Exercice : correction de l'exo posé au sujet de Métropole Septembre 2016.
- Cours : limite de suites géométriques : + preuve ROC de la limite de \(q^n\) lorsque \(q>1\) + exemple 8.
- correction de quelques exercices du manuel sur les limites de suites.
- Finir l'exo 6 de la fiche 2 .
- Jeudi 07/10 : DS n°2 sur les deux premiers chapitres : Suites et récurrence et Limites de suites.
Séance du 29/09/2016
Chapitre 2 Limites de suites
- Cours :
- Limite de suites géométriques : fin de l'exemple 8.
- Théorème de convergence monotone + exemple 9.
- Théorème de divergence monotone avec preuve ROC.
- Exercices : correction de l'exo 6 de la fiche 2 .
- correction de quelques exercices du manuel sur les limites de suites.
TD
- Exemple 10 du Cours.
- Applications des théorèmes sur les limites de suites : exos 4,3 et 5 de la fiche 2 .
- Faire l'exo 3 de la fiche 2 .
- Jeudi 06/10 : DS n°2 sur les deux premiers chapitres : Suites et récurrence et Limites de suites.
Séance du 03/10/2016
Chapitre 2 Limites de suites
- Correction d'une partie de l'exo 3 de la fiche 2 . Le corrigé complet est disponible.
Chapitre 3 Limites de fonctions
- Cours :
- Limite d'une fonction en l'infini : limite finie et asymptote horizontale + exemple 1, limite infinie et limites de références.
- Jeudi 07/10 : DS n°2 sur les deux premiers chapitres : Suites et récurrence et Limites de suites.
- Pour mardi 11/10, DM n°4 , traiter un des deux exercices au choix.
Séance du 06/10/2016
DS n°2 sur les suites, le raisonnement par récurrence, les limites de suite.
Chapitre 3 Limites de fonctions
- Cours :
- Limite d'une fonction en l'infini : limite finie et asymptote horizontale + exemple 1, limite infinie et limites de références.
- Limite d'une fonction en un réel : limite infinie et asymptote verticale + exemple 2, limite finie.
- Exercices :
- Interprétation de limite en terme d'asymptotes parallèles aux axes : exo 26 p.84.
- Finir l'exo 26 p.84.
- Pour mardi 11/10, DM n°4 , traiter un des deux exercices au choix.
Séance du 10/10/2016
Chapitre 3 Limites de fonctions
- Retour du DS n°2.
- Correction de l'exo 26 p.84.
- Cours :
- QCM de synthèse sur les limites : exemple 3.
- Règles opératoires sur les limites : tableau synopsis.
- Exercices :
- Application des règles opératoires : exos 30 p. 85 a) et b)
- Cours : Exemple 4 : Forme indéterminée de fonctions polynomes ou rationnelles.
- Pour mardi 11/10, DM n°4 , traiter un des deux exercices au choix.
Séance du 11/10/2016
Chapitre 3 Limites de fonctions
- Récolte du DM n°4.
- Exercices :
- Application des règles opératoires : exos 31 p. 85 b) et c) et 32 p. 85 a).
- Cours :
- Règles opératoires sur les limites : tableau synopsis et exemple 4 : Forme indéterminée de fonctions polynomes ou rationnelles.
Séance du 12/10/2016
Chapitre 3 Limites de fonctions
- Cours :
- Pour jeudi 11/10, finir l'exemple 6 et faire les exos 2 et 3 de la fiche 3 .
- Jeudi 03/11/2016 : DS de 2 heures sur les deux Chapitres sur les Suites et le Chapitre Limites de fonctions.
Séance du 13/10/2016
Chapitre 3 Limites de fonctions
- Cours :
- Fonction composée et limite d'une fonction composée : théorème de limite par composition,fin exemple 6, exemple 7 (composée avec \(X \mapsto \sqrt{X}\) et \(X \mapsto X^3\) )
- Théorèmes de limites par comparaison ou encadrement : théorèmes 2 et 3 et exemple 8.
AP limites de suites et de fonctions.
- Pour lundi 11/10, faire les exos 1, 6 et 7 de la fiche 3 .
- Jeudi 03/11/2016 : DS de 2 heures sur les deux Chapitres sur les Suites et le Chapitre Limites de fonctions.
Séance du 17/10/2016
- Pour lundi 07/11, DM n° 5 .
- Jeudi 03/11/2016 : DS de 2 heures sur les deux Chapitres sur les Suites et le Chapitre Limites de fonctions.
Séance du 18/10/2016
Chapitre 4 Dérivation, Primitives, Continuité
- Cours :
- 1 Dérivation d'une fonctions Définition d'une focntion dérivable en un point, équation de tangente, exemples 1 et 2.
- 2 Fonctions dérivées et opérations 2. 1 et 2.2 Régles opératoires et exemple 3
- Une fiche d'exercices sur le chapitre Dérivation et continuité avec quelques corrigés d'exercices de calculs de dérivées du manuel (13,14,15,16 p. 115).
- Pour lundi 07/11, DM n° 5 .
- Jeudi 03/11/2016 : DS de 2 heures sur les deux Chapitres sur les Suites et le Chapitre Limites de fonctions.
Toussaint
Séance du 03/11/2016
Matin : DS de 2 heures sur les deux Chapitres sur les Suites et le Chapitre Limites de fonctions.
Après-Midi : TP INFO n°2, recherche de solutions approchées d'équation par balayage ou dichotomie. Corrigé du TP en HTML. et Corrigé du TP en PDF.
- Pour lundi 07/11, DM n° 5 et terminer le TP Dichotomie pour ceux qui ne l'ont pas fait.
- Mardi 08/11 de 13h à 14 h en salles 715 et 716 : Concours Castor Informatique .
Séance du 07/11/2016
Chapitre 4 Dérivation, Primitives, Continuité
- Récolte du DM n°5.
- Retour sur le TP INFO n°2, reprise du tableau d'évolution des variables pour l'algorithme de dichotomie. Corrigé du TP en HTML. et Corrigé du TP en PDF.
- Cours :
- 2.3 Dérivée d'une fonction composée et exemple 4
- Pour mardi 08/11, dérivées de fonctions composées : faire les exos 13 2) 14 2) et 15 2) page 115
- Mardi 08/11 de 13h à 14 h en salles 715 et 716 : Concours Castor Informatique .
Séance du 08/11/2016
Chapitre 4 Dérivation, Primitives, Continuité
- Retour du DS n°3 avec son corrigé et commentaire sur l'algorithme.
- Dérivée d'une fonction composée : corrigé des exos 13 2) 14 2) et 15 2) page 115.
- Cours :
- 3 Fonction dérivée et sens de variation : théorèmes 1 et 2 et exemple 5 1) et 2) seulement.
- 4 Primitives d'une fonction :
- 4.1 Notion de primitive : définition et exemple 6 puis propriétés
- Mardi 08/11 de 13h à 14 h en salles 715 et 716 : Concours Castor Informatique .
- Pour mercredi 09/11, faire l'exemple 7 du cours et faire l'exo 3 de la fiche 4 .
- Pour mardi 15/11, DM n°6 à rédiger par groupe de deux.
Séance du 09/11/2016
Chapitre 4 Dérivation, Primitives, Continuité
- Cours :
- 4 Primitives d'une fonction :
- 4.1 Notion de primitive : exemple 7.
- 4.2 Calculs de primitive : propriété 6 puis exemple 8
- 4 Primitives d'une fonction :
- Mardi 15/11 de 12h à 13 h en salle 715 : Concours Castor Informatique .
- Pour jeudi 10/11, faire l'exo 7 de la fiche 4 .
- Pour mardi 15/11, DM n°6 à rédiger par groupe de deux.
Séance du 10/11/2016
Chapitre 4 Dérivation, Primitives, Continuité
- Calculs de primitives : fin de l'exemple 8.
- 5 Continuité :
- Définition et exemples de fonctions présentant des discontinuités (exemple 9).
- Un exemple de fonctions affines par morceaux : exemple 10.
- Règles opératoires : on justifiera dans 99 % des cas la continuité par la dérivabilité.
- Théorème des valeurs intermédiaires : exemple 13.
- Corollaires du TVI, théorème de la bijection, exemple 14.
- Recherche d'une solution approchée d'une équation par dichotomie, exemple 15. Voici le corrigé .
- Exercices de la fiche 4 : exo 8 (dichotomie et étude d'une fonction avec fonction auxiliaire). Voici un corrigé de l'application de l'algorithme de dichotomie dans l'exo 8.
Après-midi : AP sur Dérivation, Limites, Suites
- Pour lundi 14/11, faire l'exemple 15 du cours et finir l'exo 8 de la fiche 4
- Mardi 15/11 de 12h à 13 h en salle 715: Concours Castor Informatique .
- Pour mercredi 16/11, DM n°6 à rédiger par groupe de deux.
Séance du 14/11/2016
Chapitre 4 Dérivation, Primitives, Continuité
- Fin de la correction de l'exo 8 (dichotomie et étude d'une fonction avec fonction auxiliaire) de la fiche 4 : . Voici un corrigé de l'application de l'algorithme de dichotomie dans l'exo 8.
Chapitre 5 Fonction exponentielle
- Cours :
- Preuve de l'unicité de la fonction \(f\) dérivable sur \(\mathbb{R}\) telle que \(\begin{cases} f'=f \\ f(0) = 1\end{cases}\) puis définition de la fonction \( x \mapsto \text{exp}(x)\)
- Exemple 1 : tabulation de la fonction exponentielle sur la calculatrice, ordre de grandeur et conjectures sur le comportement asymptotique.
- Pour mardi 15/11 : calculs de dérivées avec la fonction exponentielle, exos 21, 23 b) et 24 b) page 148.
- Mardi 15/11 de 12h à 13 h en salle 715: Concours Castor Informatique .
- Pour mercredi 16/11, DM n°6 à rédiger par groupe de deux.
- Pour jeudi 24/11 : DS n°4 sur les chapitres Limites, Dérivation et Coninuité et Exponentielle (jusqu'à la propriété 5 du cours).
Séance du 15/11/2016
Chapitre 5 Fonction exponentielle
- Cours :
- Preuve de l'unicité de la fonction \(f\) dérivable sur \(\mathbb{R}\) telle que \(\begin{cases} f'=f \\ f(0) = 1\end{cases}\) puis définition de la fonction \( x \mapsto \text{exp}(x)\)
- Exemple 2 : étude des variations de quelques fonctions associées à la fonction exponentielle : \(f:x \mapsto \left(1+2 \, \text{exp}(x)\right)^{50}-100 \, \text{exp}(x)\) et \(g: t \mapsto \frac{\text{exp}(t)}{2} \left(2 t^{2} - 4 t + 6\right) + \frac{3}{2} \left(\text{exp}(t)\right)^2\). On réinsvestit les formules de dérivation de fonctions composées.
- Exercices : correction des calculs de dérivées des exos exos 21, 23 b) et 24 b) page 148.
- Cours :
- Propriétés algébriques : preuves ROC de \( \text{exp}(a+b)=\text{exp}(a)\times \text{exp}(b)\) et de \( \text{exp}(na)=(\text{exp}(a))^n\).
- Notation \(\text{e}^{x} = \text{exp}(x) \) et application des propriétés algébriques à l'exemple 3.
Séance du 17/11/2016
Chapitre 5 Fonction exponentielle
- Cours :
- Notation \(\text{e}^{x} = \text{exp}(x) \) et application des propriétés algébriques à l'exemple 4.
- Etude de la fonction exponentielle : sens de variation, limites aux bornes (preuve ROC) puis application dans l'exemple 6.
- Résolution d'équations ou d'inéquations : méthode puis exemples 7 et 9 (question ouverte)
- Corrigé de l'exo 3 de la fiche fiche 4
- Pour lundi : faire l'exo 2 (question ouverte) de la Fiche n°5 .
- Pour jeudi 24/11 : DS n°4 sur les chapitres Limites, Dérivation et Coninuité et Exponentielle (jusqu'à la propriété 5 du cours).
Séance du 21/11/2016
Chapitre 5 Fonction exponentielle
- Retour du DM n° 6 avec son corrigé.
- Cours :
- Résolution d'équations ou d'inéquations : fin de la correction de l'exemple 9 (question ouverte) puis exemple 8 (changement d'inconnue \(X = \text{e}^x\))
- Correction de l'exo 2 (question ouverte) de la Fiche n°5 (pas terminé).
- Corrigé de l'exo 3 de la fiche fiche 4
- Pour mardi : reprendre et finir l'exo 2 de la Fiche n°5 .
- Pour jeudi 24/11 : DS n°4 sur les chapitres Limites, Dérivation et Coninuité et Exponentielle (jusqu'à la propriété 5 du cours).
Séance du 22/11/2016
Chapitre 5 Fonction exponentielle
- Fin de la correction de l'exo 2 (question ouverte) de la Fiche n°5 (pas terminé).
- Cours :
- Croissance comparée de la fonction exponentielle avec la fonction \(x \mapsto x\) : preuve ROC puis exemple 10 d'application .
- Corrigé de l'exo 3 de la fiche fiche 4
- Fiche d'exercices supplémentaires sur l'exponentielle avec Corrigé de l'exo 4
- Pour mercredi : finir les exemples 10 et 11 du cours.
- Pour jeudi 24/11 : DS n°4 sur les chapitres Limites, Dérivation et Coninuité et Exponentielle (jusqu'à la propriété 5 du cours).
Séance du 23/11/2016
- Pour mardi prochain : DM n°7 sur l'exponentielle
- Pour jeudi 24/11 : DS n°4 sur les chapitres Limites, Dérivation et Coninuité et Exponentielle (jusqu'à la propriété 5 du cours).
Séance du 24/11/2016
DS n° 4 sur Limites, Dérivation, Continuité, Exponentielle.
Chapitre 5 Fonction exponentielle
TD sur la fonction exponentielle.
- Cours :
- Fonctions composées \( x \mapsto \text{e}^{u(x)}\) : formule de dérivation dérivation.
- Application de la formule de dérivation de \( x \mapsto \text{e}^{u(x)}\) : exo 4 de la Fiche d'exercices supplémentaires sur l'exponentielle .
- Exo 5 de la Fiche n°5 .
- Ici, un Corrigé des des exos 4 et 7 de la Fiche d'exercices supplémentaires sur l'exponentielle etde l'exo 1 Fiche n°5 .
- Pour lundi, finir l'exo 5 de la Fiche n°5 , préparer l'exo 7 de la Fiche d'exercices supplémentaires sur l'exponentielle .
- Pour jeudi prochain : DM n°7 sur l'exponentielle
Séance du 28/11/2016
Chapitre 5 Fonction exponentielle
- Fin de la correction de l'exo 5 de la Fiche n°5 .
- Cours :
- Fonctions \(x \mapsto \text{e}^{-kx}\) et \(x \mapsto \text{e}^{-kx^2}\) puis exemple 14 (Métropole Septembre 2016)
- Fiche d'exercices n°3 sur l'exponentielle : des extraits d'exercices tout chauds posés en Novembre 2016 en Amérique du Sud et en Nouvelle Calédonie.
- Ici, un Corrigé des des exos 4 et 7 de la Fiche d'exercices supplémentaires sur l'exponentielle et de l'exo 1 Fiche n°5 .
- Pour mardi, finir l'exemple 14 et faire l'exercice 2 de la Fiche d'exercices n°3 .
- Pour jeudi prochain : DM n°7 sur l'exponentielle
Séance du 29/11/2016
Chapitre 5 Fonction exponentielle
- Cours : correction exemple 14 (Métropole Septembre 2016)
- Cours : calculs de primitives des fonctions de type \(u'\text{e}^{u}\) puis exemple 15.
- Correction de l'exercice 2 de la Fiche d'exercices n°3 sur l'exponentielle : des extraits d'exercices tout chauds posés en Novembre 2016 en Amérique du Sud et en Nouvelle Calédonie.
- Ici, un Corrigé des des exos 4 et 7 de la Fiche d'exercices supplémentaires sur l'exponentielle et de l'exo 1 Fiche n°5 .
- Pour mardi, finir l'exemple 14 et faire l'exercice 2 de la Fiche d'exercices n°3 .
- Pour jeudi prochain : DM n°7 sur l'exponentielle
Séance du 01/12/2016
Chapitre 6 Probabilités conditionnelles
- Récolte du DM n°7 sur l'exponentielle .
- Cours :
-
1 Rappels :
- 1. Lois de probabilité sur un univers fini : propriétés + exemple 1
- 1. Variables aléatoires discrètes : propriétés + exemple 2
- 2 . Probabilités conditionnelles : exemple 3 (introduction) + définition + propriété +
-
1 Rappels :
- Exercice sur les probabilités conditionnelles : exo 7 p. 368 .
TD Probabilités conditionnelles et probabilités totales.
Exercices sur la Fiche d'exercices n°1 sur les probabilités conditionnelles.- Exercice 1 : probabilités conditionnelles et variables aléatoires, fiabilité d'un test de dépistage.
- Exercice 2 : probabilités conditionnelles et variables aléatoires, conformité de batteries.
- Exercice 3 : loi géométrique tronquée.
- Vendredi 02/12/2016 : cours de 17 h à 18 h en salle 822.
- Pour vendredi faire l'exemple 4 du cours.
Séance du 02/12/2016
Chapitre 6 Probabilités conditionnelles
- Cours :
- 2 . Probabilités conditionnelles : exemple 4 + arbres pondérés + exemple 5.
- 3 Formule des probabilités totales : partitions et probabilités totales : définition et propriété puis exemple 7 (Amérique du Nord juin 2016).
- Pour lundi 05/12/2016 : finir l'exemple 7 (dernière question) et préparer l'exercice 2 de la Fiche d'exercices n°2 .
Séance du 05/12/2016
Chapitre 6 Probabilités conditionnelles
- Cours :
- 3 Formule des probabilités totales : partitions et probabilités totales : correction de la dernière question de l'exemple 7 (Amérique du Nord juin 2016).
- Exercices sur la Fiche d'exercices n°2 sur les probabilités conditionnelles.
- Correction de l'exercice 2, extrait du sujet Centres-Etrangers juin 2015.
- Cours : 4.1 Indépendance de deux événements : Définition, Exemple 8 (différence entre indépendance et incompatibilité) puis Propiété 6 (preuve demain).
- Pour mardi 06/12/2016 : préparer l'exemple 9 du cours et l'exercice 5 de la Fiche d'exercices n°2 .
Séance du 06/12/2016
Chapitre 6 Probabilités conditionnelles
- Retour du DM n°7.
- Cours :
- Cours : 4.1 Indépendance de deux événements : Définition, puis Propriété 6 (preuve ROC) puis exemple 9.
- Exercices sur la Fiche d'exercices n°2 sur les probabilités conditionnelles.
- Correction de l'exercice 5, extrait du sujet Métropole Juin 2012.
- Cours : 4.2 Répétition d'expériences indépendantes 4.3 Loi binomiale et exemples 10.
- Pour mercredi 07/12/2016 : préparer le QCM 67 p. 379 et finir les exemples 10 et 11 du cours.
- Pour mardi 14/12, DS sur l'exponentielle et les probabilités conditionnelles. Revoir aussi la dichotomie et les suites (récurrence, théorème de convergence monotone).
Séance du 07/12/2016
Chapitre 6 Probabilités conditionnelles
- Cours :
- 4.3 Loi binomiale : correction des exemples 10 et 11
- Pour jeudi 08/12/2016 : faire l'exo 3 de la Fiche d'exercices n°2 .
- Pour mardi 13/12, DS sur l'expoenntielle et les probabilités conditionnelles. Revoir aussi la dichotomie et les suites (récurrence, théorème de convergence monotone).
Séance du 08/12/2016
Chapitre 6 Probabilités conditionnelles
- Exercices sur la Fiche d'exercices n°2 sur les probabilités conditionnelles :
- Exercice 1.
- Correction du QCM 67 p. 379
Chapitre 7 Nombres complexes, Partie 1
- Introduction des nombres complexes par l'équation de Bombelli \(x^3 - 15 x - 4 = 0 \)
- Cours : 1 Forme algébrique des nombres complexes :
- théorèmes / définitions 1 et 2 et exemple 1
- Pour lundi 12/12 : faire l'exo 1 de la Fiche d'exos n° 1 sur les Complexes
- Pour mardi 13/12, DS sur l'exponentielle et les probabilités conditionnelles. Revoir aussi la dichotomie et les suites (récurrence, théorème de convergence monotone).
Séance du 12/12/2016
Chapitre 7 Nombres complexes, Partie 1
- Cours : 1 Forme algébrique des nombres complexes :
- Somme et produit dans \(\mathbb{C} \) : définition et exemple 2
- Conjugué d'un nombre complexe : définition, propriété, exemples 3 et 4
- Inverse et quotient dans \(\mathbb{C} \) : propriété et exemple 5 (début).
- Corrigé des exemples du Cours sur les Complexes Partie 1
- Pour mardi 13/12, DS sur l'exponentielle et les probabilités conditionnelles. Revoir aussi la dichotomie et les suites (récurrence, théorème de convergence monotone).
- Pour jeudi 15/12 : faire les exos 1 et 2 de la Fiche d'exos n° 1 sur les Complexes et finir l'exemple 5 du cours.
- Pour le mardi 03/01 : DM n° 8
Séance du 13/12/2016
DS n° 5 : Exponentielle et probabilités.
- Pour mardi 13/12, DS sur l'exponentielle et les probabilités conditionnelles. Revoir aussi la dichotomie et les suites (récurrence, théorème de convergence monotone).
- Pour jeudi 15/12 : faire les exos 1 et 2 de la Fiche d'exos n° 1 sur les Complexes et finir l'exemple 5 du cours.
- Pour le mardi 03/01 : DM n° 8
Séance du 15/12/2016
Chapitre 7 Nombres complexes, Partie 1
- Cours : 1 Forme algébrique des nombres complexes :
- Inverse et quotient dans \(\mathbb{C} \) : exemple 5.
- Règles de calcul avec les conjugués : Propriété avec preuve ROC puis exemple 6 (Application de la propriété de caractérisation des réels ou des imaginaires purs à l'aide du conjugué).
- Mise à jour de la Fiche d'exos n° 1 sur les Complexes
- Corrigé des exemples du Cours sur les Complexes Partie 1
AP : TP INFO n°3 : marche aléatoire.
- Pour le mardi 03/01 : DM n° 8
Noel
Séance du 03/01/2017
Chapitre 7 Nombres complexes, Partie 1
- Retour du DS n°5.
- Récolte du DM n° 8.
- Cours : 1 Forme algébrique des nombres complexes :
- Règles de calcul avec les conjugués : fin de l'exemple 6 (Application de la propriété de caractérisation des réels ou des imaginaires purs à l'aide du conjugué).
- Equations du second degré à coefficients réels : théorème + exemple 7.
- Corrigé des exemples du Cours sur les Complexes Partie 1
- Mise à jour de la Fiche d'exos n° 1 sur les Complexes
- Pour mercredi 04/01 : exos 2,3 6 de la Fiche d'exos n° 1 sur les Complexes .
- Lundi 16/01 ou Mardi 17/01 : devoir d'une heure sur le chapitre Nombres Complexes Partie I.
- Mercredi 25/01 de 10 h à 12 h : Devoir Commun de deux heures sur tous les chapitres jusqu'aux Nombres Complexes inclus.
Séance du 04/01/2017
Chapitre 7 Nombres complexes, Partie 1
- Cours : fin de l'exemple 8 (Métropole juin 2014).
- Mise à jour de la Fiche d'exos n° 1 sur les Complexes
- Exercices de la Fiche d'exos n° 1 sur les Complexes , correction :
- Exo 2 : ensemble de points \(M(z) \) avec \(z = x + i y \) tels que \( \frac{x + i y }{x+ i (y -1)}\) est un réel pur ou un imaginaire pur.
- Pour jeudi 05/01 : exo 7 de la Fiche d'exos n° 1 sur les Complexes .
- Pour mardi 10/01 : DM n° 9
- Lundi 16/01 ou Mardi 17/01 : devoir d'une heure sur le chapitre Nombres Complexes Partie I.
- Mercredi 25/01 de 10 h à 12 h : Devoir Commun de deux heures sur tous les chapitres jusqu'aux Nombres Complexes inclus.
Séance du 05/01/2017
Matin
Chapitre 7 Nombres complexes, Partie 1
- Mise à jour de la Fiche d'exos n° 1 sur les Complexes
- Exercices de la Fiche d'exos n° 1 sur les Complexes , correction :
- Exo 2 : ensemble de points \(M(z) \) avec \(z = x + i y \) tels que \( \frac{z + 8 i }{z + 6}\) est un réel pur ou un imaginaire pur
- Exo 4 : récurrence.
- Exo 6 : équations du second degré.
Chapitre 8 Trigonométrie
- Cours : 1. Définitions et dérivabilité
- 1. 1 Définitions, rappels des propriétés liées au cercle trigonométrique
- 1.2 Dérivabilité, propriétés + exemple 1.
Après-Midi : AP, fiche d'exercices
- Pour mardi 10/01 : DM n° 9
- Lundi 16/01 ou Mardi 17/01 : devoir d'une heure sur le chapitre Nombres Complexes Partie I.
- Mercredi 25/01 de 10 h à 12 h : Devoir Commun de deux heures sur tous les chapitres jusqu'aux Nombres Complexes inclus.
Séance du 09/01/2017
Chapitre 8 Trigonométrie
- Retour sur l'algorithme de fiche d'AP du jeudi 05/01
- Déterminer la limite de \(f\) en 0.
- Déterminer les variations de \(f \) sur l'intervalle \( ] 0; \frac{\pi}{2} ] \) .
- Démontrer que l'équation \( f(x) = 0 \) possède une unique solution sur \( ] 0; \frac{\pi}{2} ] \) puis déterminer un encadrement de cette solution d'amplitude \( 0,01 \).
Exercice Soit la fonction \(f: x \mapsto \sin(x) - \frac{1}{3x^3} \) définie sur \( ] 0; \frac{\pi}{2} ] \)
- Pour mardi 10/01 : DM n° 9
- Lundi 16/01 ou Mardi 17/01 : devoir d'une heure sur le chapitre Nombres Complexes Partie I.
- Mercredi 25/01 de 10 h à 12 h : Devoir Commun de deux heures sur tous les chapitres jusqu'aux Nombres Complexes inclus.
Séance du 10/01/2017
Chapitre 8 Trigonométrie
- Récolte du DM n° 9.
- Cours :
- 1. Définitions et dérivabilité
- 1.2 Dérivabilité, propriétés + exemple 1.
- 1.3 Variations et signes des fonctions sinus et cosinus.
- 2 Parité et périodicité : définitions, propriété et , construction des courbes des fonctions sinus et cosinus.
- 1. Définitions et dérivabilité
- Exercices de la fiche d'exercices de Trigonométrie : exercice 1.
- Pour jeudi 12/01 : finir l'exercice 1 et faire l'exercice 2 de la fiche d'exercices de Trigonométrie .
- Mardi 17/01 : de 11 h à 12 h, devoir d'une heure sur le chapitre Nombres Complexes Partie I.
- Mercredi 25/01 de 10 h à 12 h : Devoir Commun de deux heures sur tous les chapitres jusqu'aux Nombres Complexes inclus.
Séance du 12/01/2017
Chapitre 8 Trigonométrie
- Correction de la fin de l'exercice 1 de la fiche d'exercices de Trigonométrie .
- Cours :
-
- 1. Définitions et dérivabilité 1.4 Calculs de primitives : propriété et exemple 2
- 2.2 Périodicité : exemple 3
- 2.3 Propriétés de symétrie.
- 3 Applications : 3.1 Calculs de limites : exemple 4 (théorèmes de limites par comparaison ou encadrement).
-
- Correction de l'exercice 2 de la fiche d'exercices de Trigonométrie .
TP INFO n°4
- Voici le corrigé
- Ci-dessous une petite animation maison réalisée avec Python.
- Pour lundi 16/01 : préparer l'exemple 5 1) 2) 5), l'exemple 6 et l'exemple 7 du Chapitre 8 Trigonométrie .
- Mardi 17/01 : de 11 h à 12 h, devoir d'une heure sur le chapitre Nombres Complexes Partie I.
- Mercredi 25/01 de 10 h à 12 h : Devoir Commun de deux heures sur tous les chapitres jusqu'aux Nombres Complexes inclus.
Séance du 16/01/2017
Chapitre 8 Trigonométrie
- Retour sur l'algorithme de l'exo 1 du DM n° 9 .
- Cours :
-
- 3 Applications :3.2 Lignes trigonométriques 3.2.1 Rappels sur les résolutions de \( \cos x = k \) et \( \sin x = k \) : correction de l'exemple 5 puis des exemples de résolution de \( \cos x > k \) et \( \sin x > k \) à l'aide du cercle trigonométrique (exemples 6 et 7).
-
- Correction de l'exercice 2 de la fiche d'exercices de Trigonométrie .
- Mardi 17/01 : de 11 h à 12 h, devoir d'une heure sur le chapitre Nombres Complexes Partie I.
- Mercredi 25/01 de 10 h à 12 h : Devoir Commun de deux heures sur tous les chapitres jusqu'aux Nombres Complexes inclus.
Séance du 17/01/2017
Chapitre 9 Logarithme népérien
- Cours :
- 1 Fonction logarithme népérien : définition de \(\ln x : \mapsto \ln(x) \) sur \(]0 ; + \infty[ \), exemple 1 (ensembles de définition)
- propriété : La fonction \( \ln \) est la fonction réciproque de la fonction exponentielle : \( \text{e}^{x} = y \leftrightarrow x = \ln (y) \) et exemple 2
- 1.2 Dérivée et sens de variation : propriété + exemple 3.
DS d'une heure sur les Nombres Complexes.
- Pour mercredi 18/01 :
- Etude des variations d'une fonction : exos 35 et 36 p. 185.
- Mercredi 25/01 de 10 h à 12 h : Devoir Commun de deux heures sur tous les chapitres jusqu'aux Nombres Complexes inclus.
Séance du 18/01/2017
Chapitre 9 Logarithme népérien
- Cours :
- 1.2 Dérivée et sens de variation : propriété + exemple 3 (fin).
- Résolution d'équations et d'inéquations : exemple 4 (pas terminé).
- Pour jeudi 19/01 :
- Finir l'exemple 4 et préparer l'exemple 5.
- Mercredi 25/01 de 10 h à 12 h : Devoir Commun de deux heures sur tous les chapitres jusqu'aux Nombres Complexes inclus.
Séance du 19/01/2017
Chapitre 9 Logarithme népérien
- Exercices : étude des variations d'une fonction : correction des exos 35 et 36 p. 185.
- Cours :
- Résolution d'équations et d'inéquations : exemple 4 fin).
- Cours :
- 1.3 Tangente au point d'abscisse 1
- 2 Propriétés algébriques 2.1 Propriété fondamentale Exemple 5 : une première preuve (étude de \( x \mapsto \ln(ax) - \ln(a) - \ln(x) \)) puis Preuve ROC à partir des propriétés algébriques de l'exponentielle puis Exemple 6 (Vrai / Faux) puis Corollaire de la propriété fondamentale et exemple 8 (Question ouverte Pondichéry 2016).
AP
- Fin de l'exemple 8 et exemple 7 (application des propriétés algébriques).
- Pour lundi 23/01 : Finir l'exercice 1 de la fiche d'exercices .
- Mercredi 25/01 de 10 h à 12 h : Devoir Commun de deux heures sur tous les chapitres jusqu'aux Nombres Complexes inclus.
Séance du 23/01/2017
Chapitre 9 Logarithme népérien
- Exercices : étude des variations d'une fonction : correction des exos 35 et 36 p. 185.
- Cours :
- Propriétés algébriques : fin de l'exemple 8 question 3)
- 3 Courbe représentative et comportement asymptotique : 3.1 Limites 3.2 Tableau de variations complet 3.3 Croissance comparée : propriété avec preuve dans l'exemple 9. >
- Pour mardi : préparer les questions 1 et 2 dans l'exemple 10 du cours.
- Mercredi 25/01 de 10 h à 12 h : Devoir Commun de deux heures sur tous les chapitres jusqu'aux Nombres Complexes inclus.
- DM n° 9 à rendre le jeudi 02/02.
Séance du 24/01/2017
Chapitre 9 Logarithme népérien
- Exercices : étude des variations d'une fonction : correction des exos 35 et 36 p. 185.
- Cours :
- 3 Courbe représentative et comportement asymptotique : 3.1 Limites 3.2 Tableau de variations complet 3.3 Croissance comparée : calculs de limites, exemple 10 : questions a) b) c) e) f) h) i) k) seulement.
- Fonctions composées \(x \mapsto \ln\left( u(x) \right)\) notées \( \ln \circ u \) : Propriétés + Exemple 12 (Etude des variations et calculs de limites).
- Voici un corrigé des exemples 10,12 et 15 du cours .
- Calculs de primitives : Exemple 13
- Pour lundi 30/01 : faire l'exo 6 de la fiche d'exercices
- DM n° 9 à rendre le jeudi 02/02.
- Mercredi 25/01 de 10 h à 12 h : Devoir Commun de deux heures sur tous les chapitres jusqu'aux Nombres Complexes inclus, dans l'Amphithéatre.
Séance du 30/01/2017
Chapitre 9 Logarithme népérien
- Corrigé de l'exo 6 de la fiche d'exercices
- Exercices : étude des variations d'une fonction : correction des exos 35 et 36 p. 185.
- Cours :
- Voici un corrigé des exemples 10,12 et 15 du cours .
- Logarithme décimal : définition, propriété + exemple 15
- Pour mercredi 01/02 : faire l'exo 2 (QCM) de la fiche d'exercices .
- DM n° 9 à rendre le jeudi 02/02.
- Mercredi 08/02 et 08/03 : cours de 12 à 13 en salle 824, rattrapage des deux heures cours du mardi 31/01 qui sont supprimées pour cause de devoir commun de philosophie.
- Jeudi 09/02 : DS de 2 h sur les Chapitres Logarithme et trigonométrie.
Séance du 01/02/2017
Chapitre 9 Logarithme népérien
- Voici un corrigé des exemples 10,12, 14 et 15 du cours .
- Corrigé de l'exo 6 de la fiche d'exercices
- Exercices : étude des variations d'une fonction : correction des exos 35 et 36 p. 185.
- Corrigé de l'exercice 2 de la fiche d'exercices .
- Cours :
- Calculs de primitives : Propriété + Exemple 14 1) 2) 3) et 6)
Chapitre 10 Complexes Partie 2
- Cours :
- 1 Le plan complexe 1.1 Affixe d'un point : définition de l'affixe d'un point, du point image d'un complexe, exemple 1(réviions sur le calcul vectoriel et le produit scalaire dans le plan).
- 2 Module et argument d'un nombre complexe : définition, exemple 3 et propriété 3 : preuve de \( \vert z \vert \times \vert z' \vert = \vert zz' \vert\)
- Pour le jeudi 02/02: rendre le DM n° 9 , apporter le manuel et préparer les exemples 1 et 2 du Chapitre 10 Complexes Partie 2 .
- Mercredi 08/02 et 08/03 : cours de 12 à 13 en salle 824, rattrapage des deux heures cours du mardi 31/01 qui sont supprimées pour cause de devoir commun de philosophie.
- Jeudi 09/02 : DS de 2 h sur les Chapitres Logarithme et trigonométrie.
Séance du 02/02/2017
Chapitre 10 Complexes Partie 2
- Cours :
- 1 Le plan complexe 1.1 Affixe d'un point : définition de l'affixe d'un point, du point image d'un complexe, fin de la correction de l'exemple 1(réviions sur le calcul vectoriel et le produit scalaire dans le plan).
- 1 Le plan complexe 1.2 Affixe d'un vecteur : définition, propriété et coorection de l'exemple 2
- 2 Module et argument d'un nombre complexe :
- 2. 1 Module définition, exemple 3 et propriété 3 : preuve de \( \vert z \vert \times \vert z' \vert = \vert zz' \vert\) puis exemple 4 (calculs de modules et applications en géométrie.)
- 2.2 Argument d'un complexe : Définition et exemple 5
AP : Nombres complexes, module et arguments
- Fin des exemples 4 et 5 du cours.
- Modules et ensemble de points : exercice 95 page 284.
- Pour le lundi 06/02: finir l'exemple 5 du Chapitre 10 Complexes Partie 2 et préparer 87,88,89 p. 283.
- Mercredi 08/02 et 08/03 : cours de 12 à 13 en salle 824, rattrapage des deux heures cours du mardi 31/01 qui sont supprimées pour cause de devoir commun de philosophie.
- Jeudi 09/02 : DS de 2 h sur les Chapitres Logarithme et trigonométrie.
Séance du 06/02/2017
Chapitre 10 Complexes Partie 2
- Retour du devoir commun.
- Module et argument : correction des exos 87,88,89 p. 283.
- Cours :
- 2 Module et argument d'un nombre complexe :
- 2.2 Argument d'un complexe : fin de l'exemple 5 puis définition de la forme trigonométrique. Voir la Méthode pour déterminer module et argument .
- 2 Module et argument d'un nombre complexe :
- Pour le mardi 07/02: exemple 6 du Chapitre 10 Complexes Partie 2 .
- Exercice :
Soit la fonction \(f : x \mapsto \ln(3 + \sin(x) \cos(x) ) \) . Justifier que \(f\) est définie et dérivable sur \(\mathbb{R} \) et déterminer une équation de la tangente à sa courbe au point d'abscisse 0.
- Pour le jeudi 16/02 : rendre le DM n°11
- Mercredi 08/02 et 08/03 : cours de 12 à 13 en salle 824, rattrapage des deux heures cours du mardi 31/01 qui sont supprimées pour cause de devoir commun de philosophie.
- Jeudi 09/02 : DS de 2 h sur les Chapitres Logarithme et trigonométrie.
Séance du 07/02/2017
Chapitre 10 Complexes Partie 2
- Correction de l'exercice suivant :
Soit la fonction \(f : x \mapsto \ln(3 + \sin(x) \cos(x) ) \) . Justifier que \(f\) est définie et dérivable sur \(\mathbb{R} \) et déterminer une équation de la tangente à sa courbe au point d'abscisse 0.
- Cours :
- 2 Module et argument d'un nombre complexe :
- 2.2 Argument d'un complexe : Voir la Méthode pour déterminer module et argument et correction de l'exemple 6 puis propriétés des arguments avec preuve ROC de \(\text{arg}(zz') = \text{arg}(z) + \text{arg}(z') \mod 2 \pi \) et exemple 7.
- 2.3 Nombres complexes et géométrie : propriétés 5 et 6
- 2 Module et argument d'un nombre complexe :
- Pour mercredi 08/02 : faire l'exemple 8 du Chapitre 10 Complexes Partie 2 .
- Pour le jeudi 16/02 : rendre le DM n°11
- Mercredi 08/02 et 08/03 : cours de 12 à 13 en salle 824, rattrapage des deux heures cours du mardi 31/01 qui sont supprimées pour cause de devoir commun de philosophie.
- Jeudi 09/02 : DS de 2 h sur les Chapitres Logarithme et trigonométrie.
Séance du 08/02/2017
Chapitre 10 Complexes Partie 2
- Cours :
- 2 Module et argument d'un nombre complexe :
- 2.3 Nombres complexes et géométrie : correction de l'exemple 8 puis exemple 9 (Liban et Antilles juin 2016).
- 3 Notation exponentielle : définition, propriétés algébriques puis exemples 10 et 11.
- 2 Module et argument d'un nombre complexe :
- Exercices sur la forme exponentielle : exercice 1 de la fiche d'exercices n°2 sur les Complexes .
- Pour le jeudi 16/02 : rendre le DM n°11
- Mercredi 08/02 et 08/03 : cours de 12 à 13 en salle 824, rattrapage des deux heures cours du mardi 31/01 qui sont supprimées pour cause de devoir commun de philosophie.
- Jeudi 09/02 : DS de 2 h sur les Chapitres Logarithme et trigonométrie.
Séance du 09/02/2017
DS n°8 sur le logarithme et la trigonométrie.
Chapitre 10 Complexes Partie 2
- Cours :
- Fin de l'exemple 9 du cours
- 3 Notation exponentielle : définition, propriétés algébriques.
- Exercices sur la forme exponentielle : exercice 1 de la fiche d'exercices n°2 sur les Complexes .
- Pour lundi 13/02 : exercices 1 et 3 de la fiche d'exercices n°2 sur les Complexes
- Pour le jeudi 16/02 : rendre le DM n°11
Séance du 13/02/2017
Chapitre 10 Complexes Partie 2
- Retour du DS N°8.
- Correction de l'exercice 3 de la fiche d'exercices n°2 sur les Complexes
- Pour mardi 13/02 : préparer l'exemple 10 du Chapitre 10 Complexes Partie 2 .
- Pour le jeudi 16/02 : rendre le DM n°11
Séance du 14/02/2017
Chapitre 10 Complexes Partie 2
- Fin de la correction de l'exercice 3 de la fiche d'exercices n°2 sur les Complexes
- Cours :
- 3 Notation exponentielle : propriétés algébriques, exemples 10 et 11.
- 3.3 Nombres complexes et trigonométrie : formules d'Euler et formules de développement \( \cos(a+b) = \cos(a) \cos(b) - \sin(a) \sin(b) \) puis exemple 12 (Polynésie Septembre 2015).
- Exercice 7 de la fiche d'exercices n°2 sur les Complexes .
Séance du 15/02/2017
Séance du 16/02/2017
Chapitre 11 Calcul intégral
- Présentation des CPGE scientifiques par M.Moynot.
- Récolte du DM n°11 .
- Cours :
- 1. Intégrale d'une fonction continue positive sur un intervalle :
- 1.1 Intégrale d'une fonction continue positive sur un intervalle : définition et exemples 1 (fonction affine) et 2 (interprétation physique avec Distance = Vitesse x Temps)
- 1.2 Encadrement de l’intégrale d’une fonction continue positive par la méthode des rectangles : exemple 3 programme pour la calculatrice (terminer la saisie pour la rentrée)
- 1. Intégrale d'une fonction continue positive sur un intervalle :
AP
Chapitre 10 Complexes Partie 2
- Exercices 7 et 8 de la fiche d'exercices n°2 sur les Complexes .
- Pour le lundi 6/03 : rendre le DM n°12 et finir l'exo 8 de la fiche d'exercices n°2 sur les Complexes .
- Mardi 14/03 : DS d'1 h sur les deux chapitres sur les Complexes.
Février
Séance du 06/03/2017
Chapitre 10 Complexes Partie 2
- Retour du DM n°11 .
- Récolte du DM n°12
- A propos du DM n°11 , retour sur les notions d'implication, contraposée et réciproque.
- Correction de l'exo 8 de la fiche d'exercices n°2 sur les Complexes .
-
Exercice Soit la fonction \(f: x \mapsto \cos\left(x - \frac{\pi}{3} \right) \) définie sur \([-\frac{2\pi}{3}; \frac{4\pi}{3} ] \)
- On pose \(\theta =x - \frac{\pi}{3} \), déterminer les variations puis le signe de la fonction \( \theta \mapsto \cos ( \theta) \) sur \([-\pi; \pi ] \).
- En déduire le signe de \(f(x) \) sur l'intervalle \([-\frac{2\pi}{3}; \frac{4\pi}{3} ] \) .
- Pour le mardi 7/03 : finir l'exercice ci-dessu et préparer l'exemple 5 du cours (calculs de primitives).
- Mercredi 08/03 : cours de 12 h à 13 h en salle 824.
- Mardi 14/03 : DS d'1 h sur les deux chapitres sur les Complexes, réviser en particulier les exercices 4 (Antilles juin 2013) et 8 (Centres-Etrangers juin 2016) de la fiche d'exercices n°2 sur les Complexes .
Séance du 07/03/2017
- Fin de la correction de l'exercice suivant :
Exercice Soit la fonction \(f: x \mapsto \cos\left(x - \frac{\pi}{3} \right) \) définie sur \([-\frac{2\pi}{3}; \frac{4\pi}{3} ] \)
- On pose \(\theta =x - \frac{\pi}{3} \), déterminer les variations puis le signe de la fonction \( \theta \mapsto \cos ( \theta) \) sur \([-\pi; \pi ] \).
- En déduire le signe de \(f(x) \) sur l'intervalle \([-\frac{2\pi}{3}; \frac{4\pi}{3} ] \) .
Chapitre 11 Calcul intégral
- Cours :
- 2 Primitive d'une fonction continue :
- 2.1 Théorème fondamental (sans preuve) : toute fonction continue positive sur I admet une primitive sur I de la forme \( x \mapsto \int_{a}^{x} f(t) \, \mathrm{dt} \) puis exemple 4.
- 2.2 Primitives d'une fonction continue sur un intervalle : preuve ROC de l'existence d'une primitive pour toute fonction continue sur I.
- 2.3 Calculs de primitives : tableaux des primitives usuelles et d'opérations sur les primitives et exemple 5.
- 2.4 Intégrale d’une fonction continue positive à l’aide d’une primitive : théorème.
- 2 Primitive d'une fonction continue :
- Pour le mercredi 8/03 : Préparer l'exo 4 de la Fiche d'exercices n° 1.
- Mercredi 08/03 : cours de 12 h à 13 h en salle 824.
- Mardi 14/03 : DS d'1 h sur les deux chapitres sur les Complexes, réviser en particulier les exercices 4 (Antilles juin 2013) et 8 (Centres-Etrangers juin 2016) de la fiche d'exercices n°2 sur les Complexes .
Séance du 08/03/2017
Chapitre 11 Calcul intégral
- Cours :
- 2 Primitive d'une fonction continue :
- 2.4 Intégrale d’une fonction continue positive à l’aide d’une primitive : exemple 6
- Intégrale et calcul d'aire, exercice : correction de l'exercice 4 puis questions 1) et 3) de l'exo 1 de la Fiche d'exercices n° 1
- 2 Primitive d'une fonction continue :
- Pour le jeudi 9/03 : Préparer la partie A de l'exo 3 de la Fiche d'exercices n° 1.
- Mercredi 08/03 : cours de 12 h à 13 h en salle 824.
- Mardi 14/03 : DS d'1 h sur les deux chapitres sur les Complexes, réviser en particulier les exercices 4 (Antilles juin 2013) et 8 (Centres-Etrangers juin 2016) de la fiche d'exercices n°2 sur les Complexes .
Séance du 09/03/2017
Chapitre 11 Calcul intégral
- Retour du DM n°12 .
- Cours :
- 3. Intégrale d’une fonction continue
- 3.1 Généralisation de la notion d’intégrale : Définition puis exemples 7 et 8 (Calculs d'intégrales).
- Intégrale et calcul d'aire, exercice : correction de l'exercice 3 Partie A de la Fiche d'exercices n° 1
- 3. Intégrale d’une fonction continue
AP Révisions d'analyse et d'algorithmique et calcul Intégral
- Révisions d'algorithmique (balayage et dichotomie) : Partie B de l'exo 3 de la la Fiche d'exercices n° 1. Voici un corrigé détaillé.
- Mardi 14/03 : DS d'1 h sur les deux chapitres sur les Complexes, réviser en particulier les exercices 4 (Antilles juin 2013) et 8 (Centres-Etrangers juin 2016) de la fiche d'exercices n°2 sur les Complexes .
Séance du 13/03/2017
Chapitre 11 Calcul intégral
- Cours :
- 3. Intégrale d’une fonction continue 3.2 Propriétés de l'intégrale
- Relation de Chasles et linéarité : propriétés et exemple 9.
- 3. Intégrale d’une fonction continue 3.2 Propriétés de l'intégrale
- Exercice 1 de la Fiche d'exercices n° 1 question 2) .
- Mardi 14/03 : DS d'1 h sur les deux chapitres sur les Complexes, réviser en particulier les exercices 4 (Antilles juin 2013) et 8 (Centres-Etrangers juin 2016) de la fiche d'exercices n°2 sur les Complexes .
Séance du 14/03/2017
Chapitre 11 Calcul intégral
- Cours :
- 3. Intégrale d’une fonction continue 3.2 Propriétés de l'intégrale
- Intégrale et inégalité : propriété 3 et exemple 10.
- 3. Intégrale d’une fonction continue 3.2 Propriétés de l'intégrale
DS d'1 h sur les Complexes
- Mercredi 15/03 : préparer l'exo 2 de la Fiche d'exercices n° 1.
Séance du 15/03/2017
Chapitre 11 Calcul intégral
- Cours :
- 3. Intégrale d’une fonction continue 3.2 Propriétés de l'intégrale
- Intégrale et inégalité : exemple 11.
- Correction de l'exercice 2. de la Fiche d'exercices n° 1.
- 3. Intégrale d’une fonction continue 3.2 Propriétés de l'intégrale
- Finir l'exo 7 de la Fiche d'exercices n° 1.
Séance du 16/03/2017
Chapitre 11 Calcul intégral
- Fin de la correction de l'exercice 2 de la Fiche d'exercices n° 1.
- Cours :
- 4. Applications du calcul intégral
- Aire entre deux courbes : Propriété et exemple 11.
- Valeur moyenne : Propriété et exemple 12.
- 4. Applications du calcul intégral
- Exercice 1 question 3) de la Fiche d'exercices n° 1.
AP Calcul intégral
- Limite d'intégrale : exercice 9 de la Fiche d'exercices n° 1.
- Aire entre deux courbes : exercice 6 de la Fiche d'exercices n° 1.
- Pour le lundi 27/03 : DM n° 13. .
Bac Blanc
Séance du 27/03/2017
Chapitre 12 Géométrie dans l'espace, partie 1
- Récolte du DM n° 13. .
- Cours :
- 1 Positions relatives de droites et de plans dans l’espace : définitions et exemple 1.
- 2. Parallélisme dans l'espace : preuve du théorème du toit et application (exemple 2)
- Constructions de sections planes : exemple 3 (pas terminé).
Méthode de construction d'une section plane d'un solide par un plan \(\mathcal{P}\)
- On choisit deux points de \(\mathcal{P}\) qui appartiennent à une même face du solide.
- On trace la droite reliant ces deux points.
- On construit les points d'intersection de cette droite avec les arêtes du solide qui lui sont coplanaires (dans la face du solide choisie à l'étape 1).
- On recommence l'étape 1 avec deux nouveaux points du plan \(\mathcal{P}\) tant qu'on n'a pas obtenu la section du solide par \(\mathcal{P}\), cette section devant être un polygone fermé.
- Pour le mercredi 29/03: Sections planes : exemples 3 et 4 du Chapitre 12 Géométrie dans l'espace, partie 1
- Pour le jeudi 30/03 : exercice 8 de la Fiche d'exercices n° 1 sur le calcul intégral
- DS le mardi 11/04 sur le Chapitre 11 Calcul intégral et le Chapitre 12 Géométrie dans l'espace, partie 1 .
- Cours supplémentaire le mercredi 05/04 pour rattraper mon absence du mardi 02/05.
Séance du 29/03/2017
Chapitre 12 Géométrie dans l'espace, partie 1
- Cours :
- Constructions de sections planes : exemples 3 et 4.
Méthode de construction d'une section plane d'un solide par un plan \(\mathcal{P}\)
- On choisit deux points de \(\mathcal{P}\) qui appartiennent à une même face du solide ou on utilise la propriété d'un plan coupant deux plans parallèles.
- On trace la droite reliant ces deux points.
- On construit les points d'intersection de cette droite avec les arêtes du solide qui lui sont coplanaires (dans la face du solide choisie à l'étape 1).
- On recommence l'étape 1 avec deux nouveaux points du plan \(\mathcal{P}\) tant qu'on n'a pas obtenu la section du solide par \(\mathcal{P}\), cette section devant être un polygone fermé.
- Constructions de sections planes : exemples 3 et 4.
- Pour le jeudi 30/03: Sections planes : exercice 7 et 6 (facultatif) de la fiche d'exos n°1 et faire l'exercice 8 de la Fiche d'exercices n° 1 sur le calcul intégral
- DS le mardi 11/04 sur le Chapitre 11 Calcul intégral et le Chapitre 12 Géométrie dans l'espace, partie 1 .
- Cours supplémentaire le mercredi 05/04 pour rattraper mon absence du mardi 02/05.
Séance du 30/03/2017
Chapitre 12 Géométrie dans l'espace, partie 1
- Cours :
- Constructions de sections planes : exemple 4 du cours (fin) et correction de l'exo 7 de la fiche d'exos n°1 .
Méthode de construction d'une section plane d'un solide par un plan \(\mathcal{P}\)
- On choisit deux points de \(\mathcal{P}\) qui appartiennent à une même face du solide ou on utilise la propriété d'un plan coupant deux plans parallèles.
- On trace la droite reliant ces deux points.
- On construit les points d'intersection de cette droite avec les arêtes du solide qui lui sont coplanaires (dans la face du solide choisie à l'étape 1).
- On recommence l'étape 1 avec deux nouveaux points du plan \(\mathcal{P}\) tant qu'on n'a pas obtenu la section du solide par \(\mathcal{P}\), cette section devant être un polygone fermé.
- Orthogonalité dans l'espace : définition, propriétés et exemple 6 (utilisation du plan médiateur.
- Vecteurs dans l'espace, notion de vecteurs coplanaires : exemple 7 (preuve que trois vecteurs sont coplanaires en les décomposant selon une base de l'espace).
AP : calcul intégral et géométrie dans l'espace.
- Repérage dans l'espace : définitions, propriétés et exemple 8 questions 1) et 2) du Cours.
- Section plane : exo 9 de la fiche d'exos n°1 .
- Constructions de sections planes : exemple 4 du cours (fin) et correction de l'exo 7 de la fiche d'exos n°1 .
- Pour le lundi 03/04 : représentations paramétriques de droites : lire la propriété 13, le Savoir Faire 6 page 309 et les exos 59 page 317 et 69 p. 318.
- DS le mardi 11/04 sur le Chapitre 11 Calcul intégral et le Chapitre 12 Géométrie dans l'espace, partie 1 .
- Cours supplémentaire le mercredi 05/04 pour rattraper mon absence du mardi 02/05.
Séance du 03/04/2017
Chapitre 12 Géométrie dans l'espace, partie 1
- Retour du DM n° 13. .
- Cours :
- Représentations paramétriques de droites : propriété 13 et exemple 9
- Exercices sur les représentations paramétriques de droites :
- Correction des exos 59 page 317 et 69 p. 318.
- Recherche des exos exos 4 (vecteurs et colinéarité) et 3 de la fiche d'exos n°1 .
- Pour le mardi 04/04 : faire les exos 3 et 4 de la fiche d'exos n°1 et l'exo 68 p. 318.
- DS le mardi 11/04 sur le Chapitre 11 Calcul intégral et le Chapitre 12 Géométrie dans l'espace, partie 1 .
- Cours supplémentaire le mercredi 05/04 pour rattraper mon absence du mardi 02/05.
Séance du 04/04/2017
Chapitre 12 Géométrie dans l'espace, partie 1
- Cours :
- Représentations paramétriques de droites : exemple 9 (fin).
- Exercices sur les représentations paramétriques de droites :
- Correction des exos 59 page 317, 69 et 68 p. 318.
- Correction des exos 4 (vecteurs et colinéarité) et 3 de la fiche d'exos n°1 .
- Cours :
- Représentations paramétriques de plans : propriété 14 et exemple 10.
- Exercices de synthèses:
- Exercice 8 de la fiche d'exos n°1 .
- Exercice 10 (Asie juin 2016) de la fiche d'exos n°1 , questions 1), 2) et 3).
- Pour le mercredi 05/04 : faire le devoir de Synthèse page 321 du manuel : exercices 98, 99, 100, 102 et 104 p. 321.
- DS le mardi 11/04 sur le Chapitre 11 Calcul intégral et le Chapitre 12 Géométrie dans l'espace, partie 1 .
- Cours supplémentaire le mercredi 05/04 pour rattraper mon absence du mardi 02/05.
Séance du 05/04/2017
Chapitre 12 Géométrie dans l'espace, partie 1
- Cours :
- Représentations paramétriques de plans : exemple 10.
- Exercices de synthèses:
- Correction de l'exercice 8 de la fiche d'exos n°1 .
- Pour le jeudi 06/04 : faire l'exercice 10 (Asie juin 2016) de la fiche d'exos n°1 , questions 1), 2) et 3); exercices conseillés : devoir de Synthèse page 321 du manuel : exercices 98, 100, 103 et 104 p. 321.
- DS le mardi 11/04 sur le Chapitre 11 Calcul intégral et le Chapitre 12 Géométrie dans l'espace, partie 1 .
Séance du 06/04/2017
Chapitre 12 Géométrie dans l'espace, partie 1
- Correction des exercices de synthèses:
- Exercice 5 de la fiche d'exos n°1 , démontrer que des plans sont coplanaires à l'aide d'une représentation paramétrique de plan.
- Exercice 10 (Asie juin 2016) de la fiche d'exos n°1 , questions 1), 2) et 3).
Chapitre 13 Lois à densité
AP
- Géométrie dans l'espace : section plane exo 6 de la fiche d'exos n°1 .
- Lois à densité : exo 1 de la Fiche Lois à densité n°1 .
- Pour le lundi 10/04 : exo 1 de la Fiche Lois à densité n°1 et faire le devoir de Synthèse page 321 du manuel : exercices 98, 100, 103 et 104 p. 321.
- DS le mardi 11/04 sur le Chapitre 11 Calcul intégral et le Chapitre 12 Géométrie dans l'espace, partie 1 .
Séance du 10/04/2017
Chapitre 13 Lois à densité
- Lois à densité : correction de l'exo 1 de la Fiche Lois à densité n°1 .
- Cours : 1 Lois de probabilité à densité
- 1.1 Contexte, introduction et exemple 1
- Pour mercredi 12/04 : préparer les exemples 2 et 3.
- DS le mardi 11/04 sur le Chapitre 11 Calcul intégral et le Chapitre 12 Géométrie dans l'espace, partie 1 .
- Pour le mardi 2/05 : DM n°15 à rendre dans mon casier.
Séance du 11/04/2017
DS n° 11 le Chapitre 11 Calcul intégral et le Chapitre 12 Géométrie dans l'espace, partie 1 .
- Pour mercredi 12/04 : préparer les exemples 2 et 3.
- Pour le mardi 2/05 : DM n°15 à rendre dans mon casier.
Séance du 12/04/2017
Chapitre 13 Lois à densité
- Lois à densité : correction de l'exo 1 de la Fiche Lois à densité n°1 .
- Cours :
- 1 Lois de probabilité à densité
- 1.2 Définition d'une fonction de densité et d'une variable à densité et exemple 2.
- 1.3 Espérance d'une loi à densité : propriété .
- Pour jeudi 13/04 : faire les exemples 3 et 4 du cours.
- Pour le mardi 2/05 : DM n°15 à rendre dans mon casier.
Séance du 13/04/2017
Chapitre 13 Lois à densité
- Lois à densité : correction de l'exo 1 de la Fiche Lois à densité n°1 .
- Cours :
- 1 Lois de probabilité à densité
- 1.3 Espérance d'une loi à densité : exemple 3.
- 2. Loi uniforme : définition, propriété et exemple 4.
- 3 Loi exponentielle :
- Définition et propriétés avec preuve ROC des calculs de \(\mathbb{P}( X \leqslant t) \) et \(\mathbb{P}( X \geqslant t) \) et calcul de l'espérance.
- Exemple 5 puis propriété de durée de vie sans vieillissement et exemple 6 (Métropole juin 2016)
AP : Lois à densité
- Exercices sur la fiche Fiche Lois à densité n°1 :
- Exercices 2 et 3 (loi exponentielle)
- Devoir de synthèse : exos 71 à 74 p. 409 du manuel.
- Pour le mardi 2/05 : DM n°15 à rendre dans mon casier.
- Pas de cours le mardi 2/05 au matin mais cours le mercredi 3/05 de 12 à 13.
Pâques
Séance du 03/05/2017
Chapitre 13 Lois à densité
- Récolte du DM n°15 .
- Retour du DS n° 11.
- Cours : loi normale centrée réduite
- Théorème de Moivre-Laplace : deux fichier Geogebra à télécharger fichier 1 et fichier 2
- Une synthèse sur l'introduction du théorème de Moivre-Laplace
- Loi normale \( \mathcal{N}(0,1) \) : définition, propriétés de symétrie.
- Loi normale \( \mathcal{N}(0,1) \) : faire les exos 8,9,10,11 p. 435.
- Pour le mardi 09/05 : DM n° 16
- Pour le mardi 16/05 : DS n°12 sur la géométrie dans l'espace et les lois à densité.
Séance du 04/05/2017
Chapitre 13 Lois à densité
- Une synthèse sur l'introduction du théorème de Moivre-Laplace
- Cours : loi normale centrée réduite \( \mathcal{N}(0,1) \)
- Loi normale \( \mathcal{N}(0,1) \) : définition, propriétés de symétrie et exemple 8.
- Calculs de probabilités pour la loi \( \mathcal{N}(0,1) \) avec la calculatrice : méthode et exemple 9.
- Cours : loi normale centrée réduite \( \mathcal{N}(0,1) \)
- Quantiles de la loi \( \mathcal{N}(0,1) \) : propriété avec preuve ROC, quantiles remarquables et calculs de quantiles d'ordre \(\alpha\) avec la machine : exemples 10 et 11.
- Espérance et écart-type de la loi \( \mathcal{N}(0,1) \).
- Exercices, calcul de probabilités pour une loi normale \( \mathcal{N}(0,1) \) avec la calculatrice ou une table : correction de l'exo 8 p. 435.
- Cours : loi normale \( \mathcal{N}(\mu,\sigma^{2}) \)
- Définition, espérance et écart-type
- Intervalles 1,2,3 \(\sigma\)
- Calculs de probabilités et de quantiles pour une loi \( \mathcal{N}(\mu,\sigma^{2}) \) : exemples 12 et 13.
- Pour le mardi 09/05 : DM n° 16
- Pour le mardi 16/05 : DS n°12 sur la géométrie dans l'espace et les lois à densité.
Séance du 09/05/2017
Chapitre 13 Lois à densité
- Une synthèse sur l'introduction du théorème de Moivre-Laplace
- Récolte du DM n° 16 .
- Retour du DM n°15 avec son corrigé.
- Cours : loi normale centrée réduite \( \mathcal{N}(0,1) \)
- Quantiles de la loi \( \mathcal{N}(0,1) \) : propriété avec preuve ROC.
- Cours : loi normale \( \mathcal{N}(\mu,\sigma^{2}) \)
- Calculs de probabilités et de quantiles pour une loi \( \mathcal{N}(\mu,\sigma^{2}) \) : exemples 13, 14 et 15.
- Lois à densité, exercices de la fiche Fiche Lois à densité n°1 :
- Lois normales : exercices 4 et 5.
- Lois à densité, exercices de la fiche Fiche Lois à densité n°2 :
- Loi normale et loi exponentielle : exercice 4.
- Pour le mercredi 10/05 :
- Préparer l'exo 5 de la Fiche Lois à densité n°2
- Exercice dicté de géométrie dans l'espace :
Exercice Soit ABCDEFGH un cube (voir figure ci-dessous ou page 351 du manuel) et I le point d'intersection de la droite (EC) et du plan (AHF). On munit l'espace du repère orthonormal \( D, \overrightarrow{DA},\overrightarrow{DC}, \overrightarrow{DH} \).
- Justifier que E et C appartiennent aux plans médiateurs des segments [HF] et [AF].
- En déduire que la droite (EC) est orthogonale au plan (AHF).
- Calculer le volume du tétraèdre EAFH.
- On rappelle que l'aire d'un triangle équilatéral de côté
a est \( \frac{a^2\sqrt{3}}{4}\), en déduire l'aire du triangle AHF puis la longueur EI. - On a \( \overrightarrow{EI}=t \overrightarrow{EC} \) avec \( t \in [0;1] \), déduire des questions précédentes les coordonnées du point I.
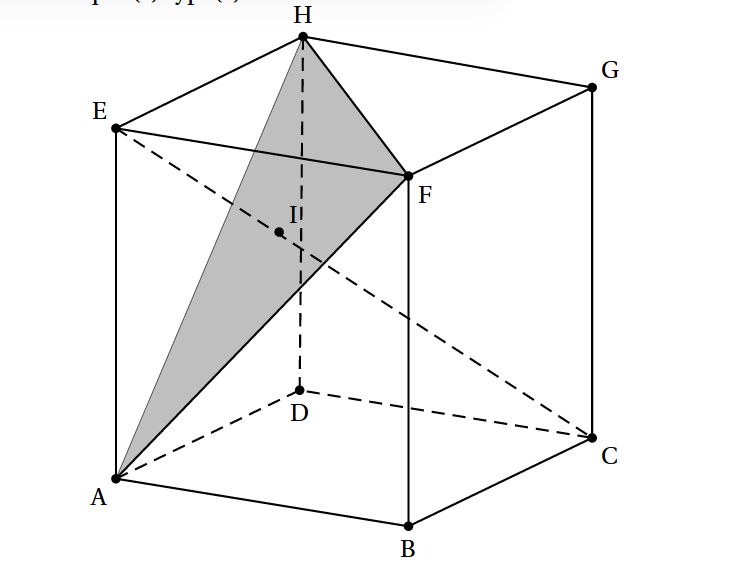
- Pour le mardi 16/05 : DS n°12 sur la géométrie dans l'espace et les lois à densité.
Séance du 10/05/2017
Chapitre 13 Lois à densité
- Une synthèse sur l'introduction du théorème de Moivre-Laplace
- Lois à densité, exercices de la fiche Fiche Lois à densité n°2 :
- Loi normale et loi exponentielle : correction de l'exercice 4.
Chapitre 14 Produit scalaire dans l'espace
- Correction de l'exercice suivant :
Exercice Soit ABCDEFGH un cube (voir figure ci-dessous ou page 351 du manuel) et I le point d'intersection de la droite (EC) et du plan (AHF). On munit l'espace du repère orthonormal \( D, \overrightarrow{DA},\overrightarrow{DC}, \overrightarrow{DH} \).
- Justifier que E et C appartiennent aux plans médiateurs des segments [HF] et [AF].
- En déduire que la droite (EC) est orthogonale au plan (AHF).
- Calculer le volume du tétraèdre EAFH.
- On rappelle que l'aire d'un triangle équilatéral de côté
a est \( \frac{a^2\sqrt{3}}{4}\), en déduire l'aire du triangle AHF puis la longueur EI. - On a \( \overrightarrow{EI}=t \overrightarrow{EC} \) avec \( t \in [0;1] \), déduire des questions précédentes les coordonnées du point I.

- Pour le jeudi 11/05 :
- Préparer les exos 1 et 2 de la Fiche Lois à densité n°2
- Pour le mardi 16/05 : DS n°12 sur la géométrie dans l'espace et les lois à densité.
Séance du 11/05/2017
Chapitre 14 Produit scalaire dans l'espace
- Cours :
- Extension du produits scalaire à l'espace : rappels et exemple 1 (preuves d'orthogonalité, calculs de distances) .
- Propriétés du produit scalaire (bilinéarité, théorème du cosinus) : rappels et exemple 2 (calcul d'angle) .
- Orthogonalité dans l'espace :
- Vecteurs orthogonaux, droites orthogonales :définition, caractérisation par le produit scalaire et exemple 3
- Droite orthogonale à un plan, vecteur normal à un plan, projeté orthogonal d'un point sur un plan ou d'un point sur une droite : définitions.
- Propriété : un droite est orthogonale à un plan ssi elle est orthogonale à toute droite de ce plan.
AP : Lois à densités et Produit Scalaire dans l'espace
- Lois à densité : exercice 5 (loi normale et loi exponentielle ) de la Fiche Lois à densité n°2 .
- Produit Scalaire (certains seulement):
- Intersection de deux droites perpendiculaires : exo 31 p. 342.
- Equation de plan : lire le Savoir Faire 5 p. 336 puis exos 39.
- Intersection droite / plan : exo 44 p. 343.
- Pour le mardi 16/05 : DS n°12 sur les chapitres Chapitre 13 Lois à densité et Chapitre 12 Géométrie dans l'espace, partie 1 .
Séance du 15/05/2017
Chapitre 14 Produit scalaire dans l'espace
- Retour du DM n° 16 .
- Cours :
- Vecteur normal, notion de projet orthogonal d'un point sur une droite ou un plan : exemple 4.
- Plans perpendiculaires : définition et exemple 5.
- Equation cartésienne d'un plan : théorème 5.
- Pour le mardi 16/05 : DS n°12 sur les chapitres Chapitre 13 Lois à densité et Chapitre 12 Géométrie dans l'espace, partie 1 .
- Pour le mardi 23/05 : DM final.
Séance du 16/05/2017
Chapitre 14 Produit scalaire dans l'espace
- Cours :
- Vecteur normal, notion de projet orthogonal d'un point sur une droite ou un plan : exemple 4.
- Equation cartésienne d'un plan : théorème 5 + exemple 6 1) 2) 3) 4) 6), différentes méthodes pour déterminer une équation de plan :
- Représentation paramétrique d'une droite orthogonale à un plan.
- point + vecteur normal ou droite orthogonale
- point + équation d'un plan parallèle
- trois points non alignés
DS n°12 sur les chapitres Chapitre 13 Lois à densité et Chapitre 12 Géométrie dans l'espace, partie 1 .
- Pour le jeudi 17/05 : préparer l'exercice 3 de la fiche Fiche Produit Scalaire n° 1 .
- Pour le mardi 23/05 : DM final.
Séance du 18/05/2017
Chapitre 14 Produit scalaire dans l'espace
- Cours :
- Equation cartésienne d'un plan : théorème 5 + exemple 6 6), différentes méthodes pour déterminer une équation de plan :
- Cas trois points non alignés
- Equation de plan et représentation paramétrique d'un plan.
- Intersection d'une droite et d'un plan : Caractérisation de leur position relative à l'aide d'un vecteur normal du plan et d'un vecteur directeur de la droite + Exemple 7.
- Intersections de deux plans :
- Caractérisation de leur position relative à l'aide des vecteurs normaux
- Equation cartésienne d'un plan : théorème 5 + exemple 6 6), différentes méthodes pour déterminer une équation de plan :
TP INFO Sujet de Pondichéry et Loi normale
- Pour le mardi 23/05 : DM final.
Séance du 22/05/2017
Chapitre 14 Produit scalaire dans l'espace
- Retour du DS n°12.
- Cours :
- Intersections de deux plans :
- Caractérisation de leur position relative à l'aide des vecteurs normaux et exemple 8.
- Système d'équations cartésiennes de droites : exemple 10 (section d'un cube par un plan d'équation donnée, d'après Pondichéry 2017). Corrigé de l'exemple 10 .
- Intersections de deux plans :
- Pour le mardi 23/05 : DM final.
Séance du 23/05/2017
Chapitre 14 Produit scalaire dans l'espace
- Récolte du DM final.
- Cours :
- Intersections de deux plans :
- Système d'équations cartésiennes de droites : exemple 9 (d'un système d'équations à une représentation paramétrique de droites).
- Intersections de deux plans :
- Correction de l'exercice 3 de la fiche Fiche Produit Scalaire n° 1 .
Chapitre 15 Echantillonnage et estimation
- Cours 1 Echantillonnage et intervalle de fluctuation :
- 1.1 Intervalle de fluctuation exact de première : réalisation d'un programme pour IFE, exemple 1.
- Pour le mercredi 24/05 : préparer l'exercice 4 de la fiche Fiche Produit Scalaire n° 1
Séance du 24/05/2017
Chapitre 15 Echantillonnage et estimation
- Cours 1 Echantillonnage et intervalle de fluctuation :
- 1.1 Intervalle de fluctuation exact de première : réalisation d'un programme pour IFE, exemple 1.
- 1.12 Intervalle de fluctuation asymptotique de terminale : corollaire de Moivre-Laplace, définition d'un intervalle de fluctuation asymptotique, conditions d'approximation, intervalle de fluctuation asymptotique au seuil de 95 %, réalisation d'un programme pour IFA puis exemple 2.
- Corrigés des exemples 1 et 2.
- Distribution de la de la fiche Fiche Echantillonnage / Estimation n° 1 .
- Pour le lundi 29/05 : préparer l'exercice 4 de la fiche Fiche Produit Scalaire n° 1 et les exemples 3 et 4 du Chapitre 15 Echantillonnage et estimation .
Séance du 29/05/2017
Chapitre 15 Echantillonnage et estimation
- Cours 1 Echantillonnage et intervalle de fluctuation :
- Corrigés des exemples 1 et 2.
- Intervalle de fluctuation asymptotique de terminale et intervalle de fluctuation de seconde.
- Intervalle de fluctuation asymptotique et prise de décision : méthode et correction des exemples 3 et 4.
- Distribution de la de la fiche Fiche Echantillonnage / Estimation n° 1 .
- Pour le mardi 30/05 : préparer les exercices 4 et 5 de la fiche Fiche Echantillonnage / Estimation n° 1 .
Séance du 30/05/2017
Chapitre 15 Echantillonnage et estimation
- Cours 1 Echantillonnage et intervalle de fluctuation :
- Corrigés des exemples 1 et 2.
- Intervalle de confiance : principe, formule et exemple 5 (Métropole juin 2016).
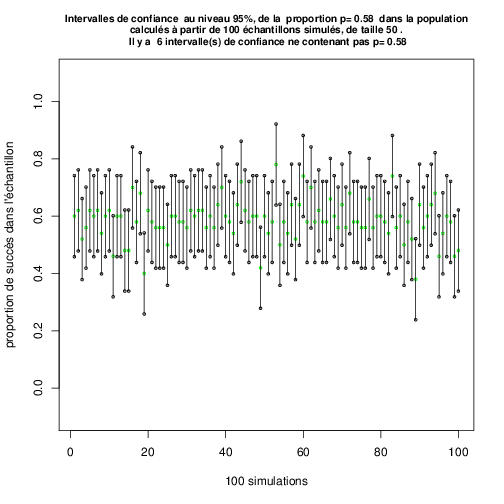
- Correction des exercices 4 et 5 de la fiche Fiche Echantillonnage / Estimation n° 1 puis recherche de l'exo 6.
- Distribution de la fiche de révisions Pondichéry 2017. et exercice 1 (Probabilités)
- Pour le jeudi 02/06 : préparer les exercices 1 et 2 de la fiche de révisions Pondichéry 2017. .
Séance du 01/06/2017
Chapitre 15 Echantillonnage et estimation
- Correction des exercices 1 (probabilités) et 2 (analyse) de la fiche de révisions Pondichéry 2017. puis recherche de l'exercice 3 (suites).
- Recherche de l'exo 8 de la fiche Fiche Echantillonnage / Estimation n° 1 puis recherche de l'exo 6.
- Correction de l'exercice 4 de la fiche Fiche Produit Scalaire n° 1 .
- Fiche de révisions n°2 , questions avec prise d'initiative.
Séance du 06/06/2017
Le Bac sur Eduscol
- Travail sur le sujet posé en Amérique du Nord le 2 juin 2017